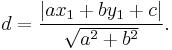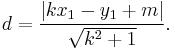Perpendicular distance

In geometry, the perpendicular distance from a point 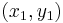(x_1, y_1) to the line ax + by + c = 0 is given by

d = \frac{|ax_1 %2B by_1 %2B c|}{\sqrt{a^2 %2B b^2}}.

If the equation of the line is given on the form y = kx + m, the perpendicular distance from 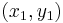(x_1, y_1) is given by

d = \frac{|k x_1 - y_1 %2B m|}{\sqrt{k^2%2B1}}.

Proof (Two Dimensions)

Consider the line given by 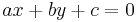ax %2B by %2B c = 0 and a point 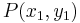P(x_1,y_1) . For ease, consider a point given by 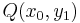Q(x_0,y_1) , where 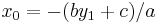x_0 = -(by_1 %2B c)/a (since 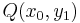Q(x_0,y_1) is on the line). Then we have

d_\perp = |PQ \sin \theta| = |(x_1 - x_0) \sin \theta| .

Here \theta is simply the angle between the line and the x-axis, such that

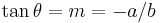\tan \theta = m = -a/b .

Using the Pythagorean theorem we have 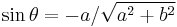\sin \theta = -a/\sqrt{a^2 %2B b^2} , and

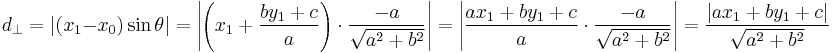d_\perp = |(x_1 - x_0) \sin \theta| = \left|\left(x_1 %2B \frac{by_1%2Bc}{a}\right) \cdot \frac{-a}{\sqrt{a^2 %2B b^2}}\right| = \left|\frac{ax_1%2Bby_1%2Bc}{a} \cdot \frac{-a}{\sqrt{a^2 %2B b^2}}\right| = \frac{|ax_1%2Bby_1%2Bc|}{\sqrt{a^2 %2B b^2}}.

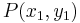This can be extended to the case where Q is any point on the line, however, one can always choose Q such that one coordinate is common to P(x_1,y_1) to simplify the formulation.

Proof (Higher Dimensions)

The general formula for higher dimensions can be quickly arrived at using vector notation. Let the hyperplane have equation 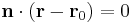\mathbf{n} \cdot (\mathbf{r} - \mathbf{r}_0) = 0 , where the 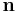\mathbf{n} is a normal vector and 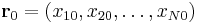\mathbf{r}_0 = (x_{10},x_{20},\dots,x_{N0}) is a position vector to a point in the hyperplane. We desire the orthogonal distance to the point 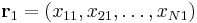\mathbf{r}_1 = (x_{11},x_{21},\dots,x_{N1}). The hyperplane may also be represented by the scalar equation 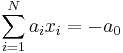\sum_{i=1}^N a_i x_i = -a_0, for constants 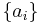\{a_i\}. Likewise, a corresponding 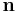\mathbf{n} may be represented as 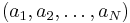(a_1,a_2, \dots, a_N). 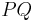The magnitude of the vector \mathbf{r}_1 - \mathbf{r}_0 is like our distance PQ above, so we desire the scalar projection in the direction of 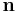\mathbf{n}. 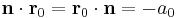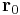Noting that \mathbf{n} \cdot \mathbf{r}_0 = \mathbf{r}_0 \cdot \mathbf{n} = -a_0 (as \mathbf{r}_0 satisfies the equation of the hyperplane) we have

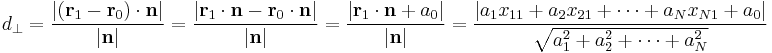d_\perp = \frac{|(\mathbf{r}_1 - \mathbf{r}_0) \cdot \mathbf{n}|}{|\mathbf{n}|} = \frac{|\mathbf{r}_1\cdot \mathbf{n} - \mathbf{r}_0 \cdot \mathbf{n}|}{|\mathbf{n}|} = \frac{|\mathbf{r}_1\cdot \mathbf{n} %2B a_0|}{|\mathbf{n}|} = \frac{|a_1x_{11} %2B a_2x_{21} %2B \dots %2B a_Nx_{N1} %2B a_0|}{\sqrt{a_1^2 %2B a_2^2 %2B \dots %2B a_N^2}}.

Notice how the general expression is consistent with 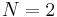N=2 dimensions.

See also